正方形と同じ面積を持つ円の共通部分の面積

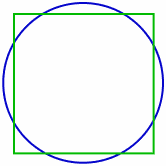（Wikipedia の円積問題のページの画像）

上の画像の正方形と円の共通部分の面積（元の面積からみた比率）を求めてみた。
いきなり答えを書くと、元の正方形もしくは円の面積が1の場合で約0.91になるみたい。

最初式を求めようと思ったけど、いっけん簡単そうに見えるものの実は不可能なものの有名な例である円積問題と関係するので、数値を入れるだけでズバッと答えが得られるような簡単な式を求めるのは無理なのではないかと思いモンテカルロ法で求めた。
いや簡単な式あるよ？って方がいましたら教えていただけると嬉しいです。

まぁ約0.91という数字が得られた今となっては単に「面積 x 0.91」を計算するだけでいいんだけど、その約0.91という数字自体の意味を知りたい。
なんか円周率が関係ありそう。

計算に使ったコードは以下のとおり。
久しぶりにPythonで書いた気がする。

square-circle-intersection-area.py

#!/usr/bin/env python
# coding: UTF-8

import random
import math

def in_circle(x, y, r2):
    return x ** 2 + y ** 2 < r2

circle_r2 = 1.0 / math.pi
in_circle_count = 0
sample_count = 10000000

for i in xrange(sample_count):
    x = random.uniform(-0.5, 0.5)
    y = random.uniform(-0.5, 0.5)
    if in_circle(x, y, circle_r2):
        in_circle_count += 1

print "in circle rate:", float(in_circle_count) / sample_count

なんでこんな事したかというと、ベイカーの直接照明の質および速度を上げるため。（あとFGでも使えるかも。）
光がテクセルに当たったときに、円形の範囲に影響を与えると仮定し、さらにテクセルを正方形と仮定すると、その円がはみ出た分は隣接テクセルにも影響を与えるべきであり、そうすることで、1テクセルあたりの光源サンプル数はそのままで陰影や影の境界がなだらかになる等、多少は質が向上するのではないかという、テキトーな思いつきが発端。

どうなることやら。